Saturday, June 20, 2020
Sunday, April 12, 2020
Monday, March 23, 2020
Tuesday, January 21, 2020
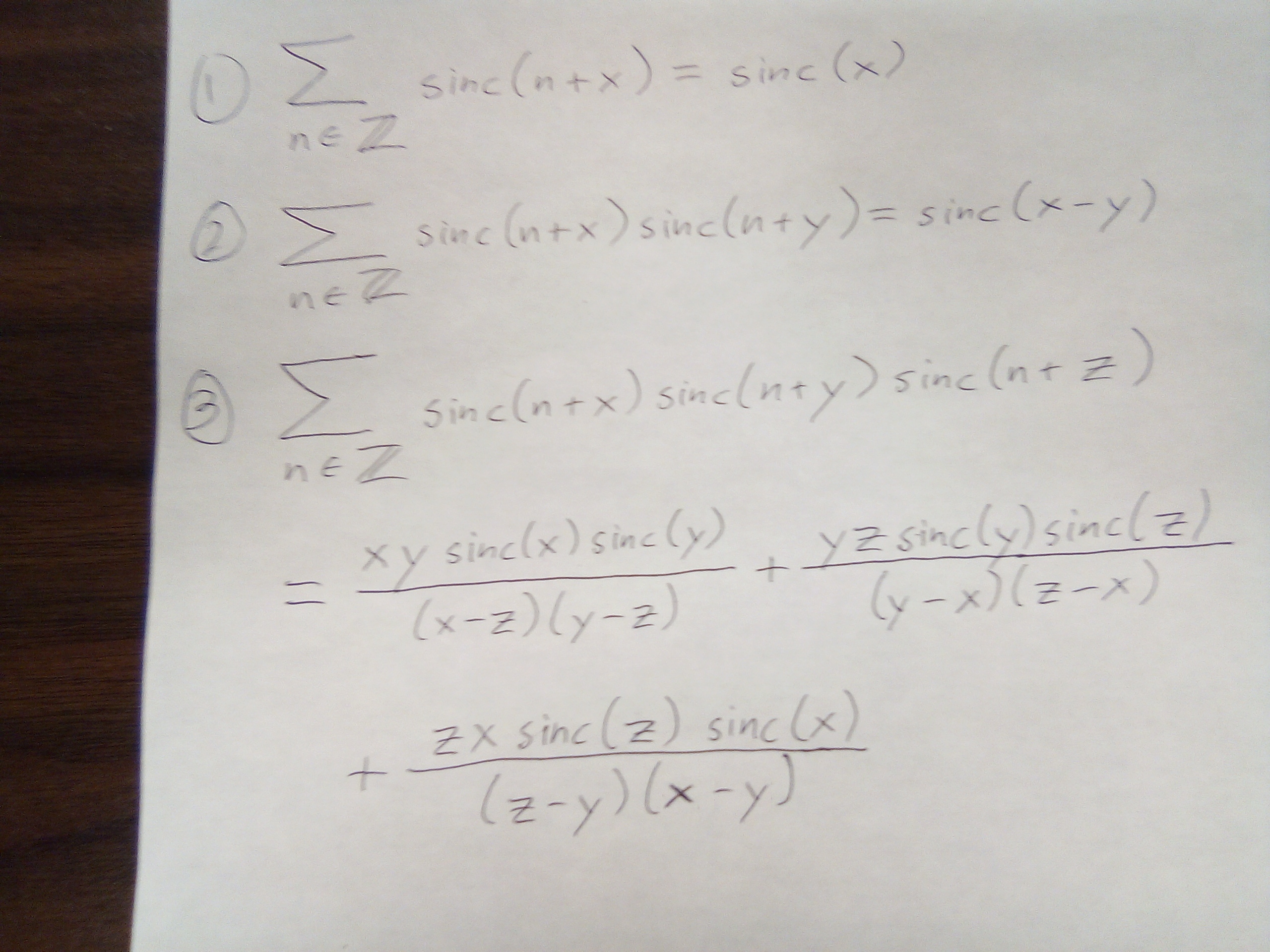
Tuesday, July 09, 2019
Friday, February 08, 2019
Monday, May 07, 2018
Saturday, April 28, 2018
Friday, April 20, 2018
I haven't seen this chain characterization in the textbooks I've used, but it's trivial to prove using a known result from infinitary order theory. (A poset is chain-complete iff it is directed-complete.) Surely, this has been done before. I just don't know where.
Rather than develop a bunch of order theory I didn't have time for in my topology class, I typed up an "elementary" proof, using "just" a well-ordering, that chain compactness is equivalent to the compactness in the usual sense.
If you know a thing or two about posets, you will recognize that the proof trivially generalizes into a proof that posets are chain-complete if and only if directed-complete. I don't know if my proof approach is new. But my recollection is that the standard proof uses induction on cardinality of the chains and directed sets, which I think is conceptually more elaborate than my approach of using a well-ordering to extract a minimal bad chain from a bad directed set.
Saturday, March 24, 2018
a one with nothing but zeros to the left, nothing but zeros above, and nothing but zeros below.Some textbooks don't require a pivot to be a one, just to be nonzero. But in any case, the books I've seen state the requirement about surrounding zeros in more complicated way.
The same day, I gave definition of reduced row echelon form simpler than what I'd seen in textbooks.
A matrix is in RREF if every nonzero row contains a pivot, the pivot rows are above the zero rows, and the pivots descend to the right.Maybe I just haven't been reading the right textbooks. I was given a review copy of Gareth Williams' textbook, but too late to use it this semester. It doesn't define pivots, but its definition of RREF matches mine, with instances of "pivot" expanded into a definition of pivot that matches mine.
Tuesday, February 06, 2018
Monday, January 29, 2018
Thursday, January 25, 2018
Friday, January 12, 2018
Tensor squares entangle.
The context involves a pair of particles which we will assume to be electrons for simplicity. Let Xn measure the spin of the nth electron with respect to the x-axis. Applying Xn will put the nth electron's spin in the +x or -x direction; the corresponding macroscopic observation will be +1 or -1 (ignoring physical units). Let Yn be the analog of Xn for the y-axis. If we measure with Xn then Yn then Xn again, then the first and second Xn measurements merely have a 1/2 chance of being the same. In general, if spin of an electron is along one axis and we measure its spin with respect to another axis, we effectively destroy information. (Technically, the information is not destroyed. But recovering it is like unscrambling an egg.)
The above information loss is algebraically manifested as Xn and Yn not commuting. However, these operators do anti-commute: XnYn=-YnXn. Therefore, assuming our two electrons' spin states are independent of each other (which is approximately true if the electrons are not too close together), a little algebra shows that the tensor products X=X1⊗X2 and Y=Y1⊗Y2 do commute. Physically, this means that if we measure with X then Y then X again, the two X measurements will agree with probability 1, not 1/2. If we physically interpret a tensor product as simply performing two measurements at the same time, then this makes no sense.
But X actually measures the product of a potential X1 measurement value and a potential X2 measurement value. This will be +1 if the X1 and X2 both output +1 or both output -1, and will be -1 otherwise. In other words, X is measuring merely whether the two particles have the same or opposite spin with respect to the x-axis. Unlike an Xn, the act of measuring X does not align either particle's spin to the x-axis (unless it was already there). Instead, applying X merely changes the joint state of the particles such that the results of potential future X1 and X2 measurements are now either perfectly correlated or perfectly anti-correlated, depending on whether X measured +1 or -1.
The bottom line is that, by measuring with X and then Y, that is, by measuring with respect to each of two perpendicular axes merely whether our two particles have the same or opposite spins, we put the two particles into one of four maximally entangled joint states with the very nice property that repeated measurements of X and Y will preserve the joint state of the electrons. If the X output changes or the Y output ever changes when performing these repeated measurements, that indicates outside "noise." This is a simple instance of quantum error detection for two qubits. With more electrons, the paper explains how to achieve quantum error correction.
Monday, January 08, 2018
Saturday, January 06, 2018
Thursday, January 04, 2018
Friday, November 24, 2017
Tuesday, November 21, 2017
Tuesday, November 14, 2017
Saturday, September 09, 2017
Tuesday, September 05, 2017
Wednesday, July 12, 2017
[T]here is a significant and fairly large (16% without covariates in the model, 14% with) difference in odds of passing the course for those randomized to the intro stats course compared to the elementary algebra course...Yep. And statistics is more directly useful for non-STEM majors who, for example, want to understand the news.I will hold with Hacker in suggesting that this does represent a lowering of standards, and that this is a feature, not a bug. That is, I think we should allow some students to avoid harder math requirements precisely because the current standards are too high. Students in deeply quantitative fields will have higher in-major math requirements anyway.
I also found it interesting that "support workshops" for remedial college algebra students didn't measurably improve pass rates in this study. I'm not sure what to make of that. I suppose it's consistent with my anecdotal, non-randomized-control-trial experience that more conscientious students are both more likely to pass and more likely to take the time to get help from tutors and/or their professors on a regular basis.
Saturday, July 08, 2017
Saturday, July 01, 2017
If the Fed wanted 2018 US NGDP to be more than $20T (for example), it could say, "whenever betting markets generally predict 2018 US NGDP under $20T, we will start to buy and hold assets of our choosing, at a rate of $1B the first day and doubling the rate every day thereafter, until betting markets generally predict 2018 US NGDP over $20T."When there is a large negative expected NGDP, the mismatch between downward-sticky wages and much more plastic hiring/firing/layoffs aggregates into a large short-term misallocation of real resources.
Therefore, the Fed should buy whatever it takes to reverse large downward surprises in expected NGDP.
Monday, June 26, 2017
I remember when the names iteration.mit.edu and recursion.mit.edu were mine; they pointed to my public IPv4 address 18.238.3.106. I don't claim to have done anything innovative with them, but what I did was very educational. I wrote a minimal http server in C++ and hosted a static website with fractal images I created and a Mandelbrot set Java applet I wrote.
I probably never would have been motivated to learn how to write an http server without such public visibility. Security risks? Yes. (I promptly fixed that one.) Despite this, MIT thrived without a NAT for many years. Even if security risks are greater today, firewalls can be made arbitrarily strict without a NAT.
Monday, June 19, 2017
A bit of TeX hacking
I've decided that if I state, say, Theorem 2.2.15 but don't prove it until many pages and lemmas later in Section 5, then, for the reader's sake, I should repeat the theorem verbatim, including the original theorem number, immediately before the proof, as opposed to going straight from the proof of Lemma 5.2.33 to "Proof of Theorem 2.2.15." (Granted, if the delay between statement and proof is just for one "Main Theorem" whose statement is easy to remember, then this is not necessary. My decision is in the context of revising a longer paper with several theorems stated early and proved much later.)
%#1 theoremstyle inpute (plain/definition/remark/...)
%#2 type of theorem (Theorem/Lemma/Corollary/...)
%#3 label of theorem to be repeated
%#4 unique new input for \newtheorem
%#5 statement of theorem
\def\repeattheoremhelper#1#2#3#4#5{
\theoremstyle{#1}
\newtheorem*{#4}{#2 \ref{#3}}
\begin{#4}
#5
\end{#4}
}
\def\repeattheorem#1#2{
\repeattheoremhelper{plain}{#1}{#2}{repeat#2}{\csname state#2\endcsname}
}
%usage example
%\theoremstyle{plain}
%\newtheorem{thm}{Theorem}
%...
%\def\statemytheorem{blah blah}
%\begin{thm}\label{mytheorem}\statemytheorem\end{thm}
%...
%\repeattheorem{Theorem}{mytheorem}
%\begin{proof}
%...
%\end{proof}
